【EV扑克】关于扑克与博弈论 你需要知道这些！附实战秘籍

【EV 扑克(http://www.evp86.com)报道】

今天给大家带来一堂博弈论基础课，大家熟悉的名词“GTO”全称即为 Game Theory Optimal-博弈论最优解。

博弈论基础

博弈论最经典的案例：囚徒困境

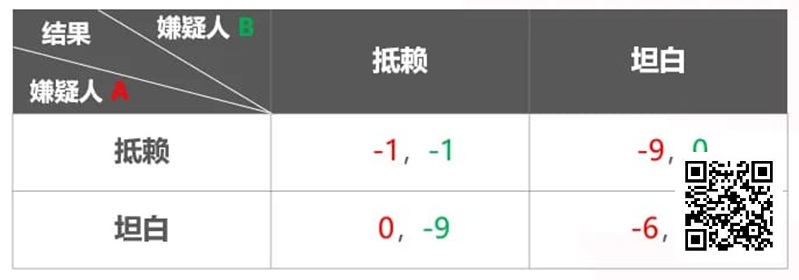
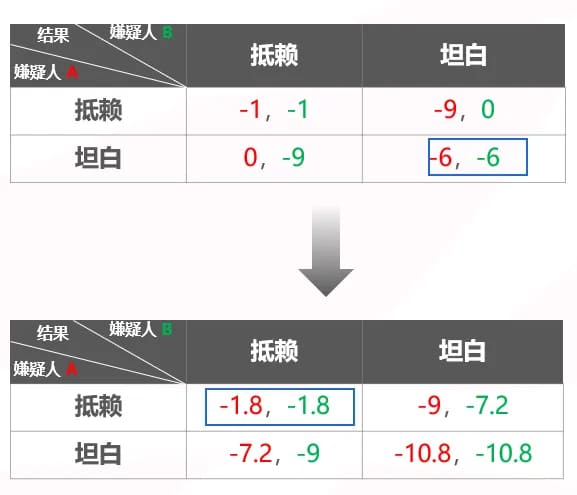
两名犯罪嫌疑人被分开审问不能串供，如果他们同时抵赖，每人将被判刑 1 年，同时招供则会被判刑 6 年；然而如果一人抵赖一人招供，则抵赖的那个人会被判 9 年，招供的人会被释放。

看起来双方都抵赖是对彼此最好的选择，然而这种最优局面能实现吗？

站在 A 的立场

如果 B 抵赖，自己抵赖的收益是-1，自己坦白的收益是 0，抵赖是不可取的

如果 B 坦白，自己抵赖的收益是-9，自己坦白的收益是-6，抵赖是不可取的

站在 B 的立场

如果 A 抵赖，自己抵赖的收益是-1，自己坦白的收益是 0，抵赖是不可取的

如果 A 坦白，自己抵赖的收益是-9，自己坦白的收益是-6，抵赖是不可取的

因此，对双方来说，抵赖都是不会被选择的策略，最终会形成双方都坦白，每人获刑 6 年的结局。

“双方都坦白”这一局面，就被称为“纳什均衡-Nash Equilibrium”。这是博弈论中最重要的概念，它的定义是：任何一个参与者单独偏离均衡点，均不会导致自己的结果变好

我们来验证一下这一定义

如果 A 单独将自己的策略从坦白变成抵赖，他的刑期将从 6 年增加到 9 年，结果变差了

同理，如果 B 单独将自己的策略从坦白变成抵赖，他的刑期将从 6 年增加到 9 年，结果变差了

以上就是博弈论中最经典囚徒困境案例，是不是很简单~

博弈论四个基本要素

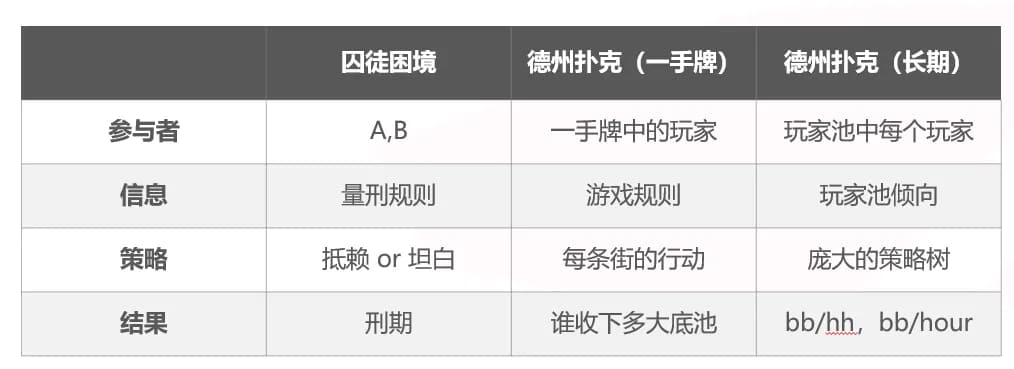
接下来我们从这个案例出发，讲一下博弈论的四个基本要素：参与者、信息、策略和结果，由这四个要素组成的问题是适合用博弈论来研究的。

显然竞技扑克是适合用博弈论来研究的，然而单一手牌和长期的扑克游戏对应的博弈论四要素其实是有差异的。

四种游戏类型：完美信息静态博弈（囚徒困境）、非完美信息静态博弈（医药）、完美信息动态博弈（围棋）、非完美信息动态博弈（竞技扑克）

根据游戏是静态还是动态的，参与者知道的信息是全面的还是不全面的，博弈论研究范畴中的游戏可以分为四类，其中竞技扑克游戏是最复杂的非完美信息动态博弈游戏。

以上是博弈论基础知识部分，有想深入学习博弈论的同学这里给大家推荐一套免费的公开课，是耶鲁大学经济学院录制的，配有中文字幕（http://open.163.com/special/gametheory/）。

这里我们就不深入讲博弈论的知识了，接下来我们就用博弈论这些最基础的知识，来重新审视一下我们熟悉的德州扑克游戏。

AKQ Toy Game

相信很多爱学习的扑克玩家都听说过 AKQ Toy Game，今天我们就带大家来完整演算一遍。

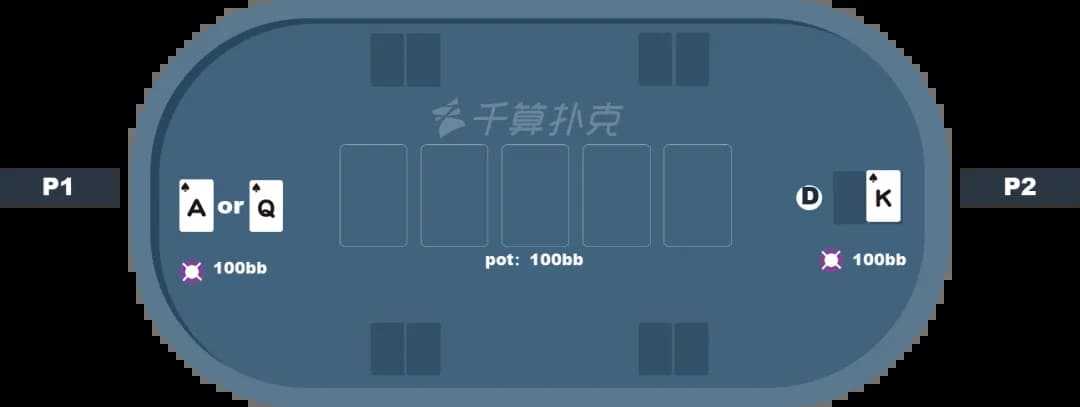
游戏规则如下：

两位玩家，没人手中一张牌，后行动的玩家 2 手牌一定是一张 K，先行动的玩家 1 手牌有 50%可能性是 A，50%可能性是 Q；且双方都知道对方的手牌分布

底池有 100bb 筹码，双方各有 100bb 筹码，双方如果选则下注，下注尺度只能选择 100bb allin

动态博弈游戏的求解过程是逆序求解，我们先来考虑后行动的玩家 P2 的策略：

如果 P1 没有下注，那么 P2 是没有理由下注的，因为面对 P2 的下注 P1 只会用 A（如果 P1 过牌范围中有的话）跟注，Q 弃牌

如果 P1 下注，那么 P2 不能 100%的跟注，因为这样的话 P1 就可以只用 A 下注

如果 P1 下注，那么 P2 不能 100%的弃牌，因为这样的话 P1 就可以只用全部的 A 和 Q 下注

综上，P2 的策略应该是：如果 P1 过牌，则随后过牌；如果 P1 下注，则以一定频率跟注，具体频率还需要计算，我们先设为未知数 y

接下来我们看 P1 的策略：

因为自己过牌后 P2 100%会过牌，而自己下注后 P2 有一定频率 y 跟注，所以 P1 手持 A 时应该 100%下注

P1 手持 Q 时不能 100%的过牌，因为这样的话 P2 就可以在面对 P1 下注时 100%弃牌来使得 P1 手持 A 下注时拿不到价值

P1 手持 Q 时也不能 100%下注，因为这样的话 P2 面对 P1 的下注范围有 50%的胜率，而 P2 跟注只需要 33%(=100/(100+100+100))，P2 可以 100%跟注自动获利

综上，P1 的策略应该是：手持 A 时间 100%下注；手持 Q 时以一定频率下注，设为未知数 x

经过以上分析，我们发现双方各自还有两个行动不确定：P1 手持 Q 的时候该以怎样的频率过牌和下注；P2 面对 P1 下注时该以怎样的频率跟注和弃牌。这四个未确定的行动各自的 EV 表达式如下：

EV(P2 Call)=300*x/(1+x)-100

EV(P2 Fold)=0

EV(P1 Bet with Q)=200*(1-y)-100

EV(P1 Check with Q)=0

两位玩家都想达到对自己最优的结果，也就是说，让对方调整他的频率并不能带来他 EV 的升高。也就是说，P1 通过给出确定的 x，让 EV(P2 Call)=EV(P2 Fold)；P2 通过给出确定的 y，让 EV(P1 Bet with Q)=EV(P1 Check with Q)

联立方程组可以解得：x=50%，y=50%

我们来总结一下双方的策略以及底池的 100bb 是如何分配到各条策略树上进而分配给两位玩家的：

P1 手持 A 时 100%下注；手持 Q 时 50%下注，50%过牌

P2 面对 P2 的过牌 100%过牌；面对 P1 下注时 50%跟注，50%弃牌

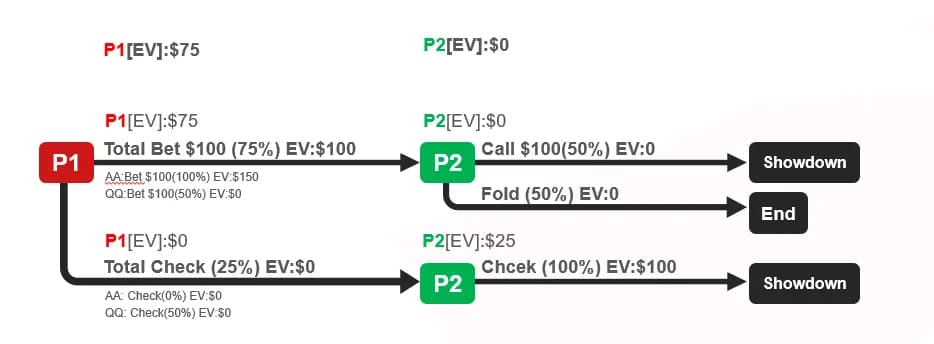
策略树在 P1 行动时分为两个分支，75%的情况下进入 P1 bet 分支，其中 P1 手持 A 的情况占 50%，Q 占 25%；另外 25%的情况进入 P1 check 的策略树分支，此时 P1 一定持有 Q。

进入 P1 check 分支后，P2 100% check，游戏结束，P2 通过摊牌 K 赢 Q 收下底池 100bb；进入 P1 bet 分支后，P2 会有两个子分支，50%的 call 和 50%的 fold，P2 fold 的 EV 显然是 0，P2 call 时，由于 P1 下注范围中的价值咋呼比是 2：1，与 P2 的抓诈赔率 2：1 相等，所以 P2 的跟注也是 0EV。

因此，只要进入 P1 bet 的策略树分支，无论 P2 是 call 还是 fold EV 都是 0，P1 收下底池全部 100bb。

我们可以看到，虽然双方范围 equity 都是 50%，但是 P1 因为手持极化范围，获得了了 75%的 EV。

囚徒困境进阶

为了后面更好的讨论如何应对跟注站和疯狂咋呼两种娱乐玩家，我们需要准备一些博弈论进阶知识。

我们刚刚提到过，博弈论游戏的四要素分别是：参与者、信息、策略和结果，这里我们默认了结果即等于收益。

如果参与者的收益不只是直接的结果，还受其他因素影响，会有什么变化呢？

回到囚徒困境的例子，如果两个犯罪嫌疑人都是“利他型”参与者，即希望对方也得到好结果，情况就会发生变化。我们给出一个新的收益公式

y1’= y1+0.8*y2

y2’= y2+0.8*y1

也就是说，嫌疑人 A 的最终收益不只是自己的获刑结果，还要加上 B 的结果乘以一个 0.8 的系数；B 也同理。这样一来，双方虽然面临四种情况不变，但是每种结果的收益发生了变化，如下图所示

在这个模型下，双方就能达成同时抵赖，结果是没人被判一年，双方收益都是-1.8 的新的纳什均衡。

如何应对跟注站老板

在 AKQ Toy Game 中，如果 P2 是跟注站玩家，情况又会发生什么变化呢？

关键是如何量化“跟注站”这一行动倾向上的偏移，并把它带入 EV 公式。

P2 之所以会从理智玩家偏移为“跟注站”，是在他的价值判断体系中，自己的 K 面对 P1 的 Q 诈唬弃牌时，不只没有赢下底池，还会额外损失 a 的情绪上的不爽，同时 P2 认为 P1 会因为诈唬成功收获这 a 的情绪价值（因为竞技扑克是零和博弈）

双方各个行动新的 EV 公式如下

EV(P2 Call)=300*x/(1+x)-100

EV(P2 Fold)=-a*x/(1+x)

EV(P1 Bet with Q)=(200+a)*(1-y)-100

EV(P1 Check with Q)=0

可以解得

y=(100+a)/(200+a)

x=100/(200+a)

如果我们作为 P1 玩家，观测到 P2 玩家的跟注频率从均衡值 50%偏移为 55%时，可以求出 P2 心目中 a 的价值是 22.22，进而可以算出我们对应的最优策略是手持 Q 时下注频率从 50%下降到 45%

注意，这是一个 P2 认知偏移前提下的均衡策略，而不是 P1 采取的最大剥削策略。从最大剥削的角度来说，如果 P2 跟注频率高于最优频率哪怕只有 1%，P1 都应该放弃全部诈唬，只做价值下注。

但是，这种最大剥削策略的漏洞十分明显，很快会被 P2 观测到并反剥削。而现在这个偏移后的均衡解，是可以长期保持的，它的本质是 P2 在为自己的错误认知付费。

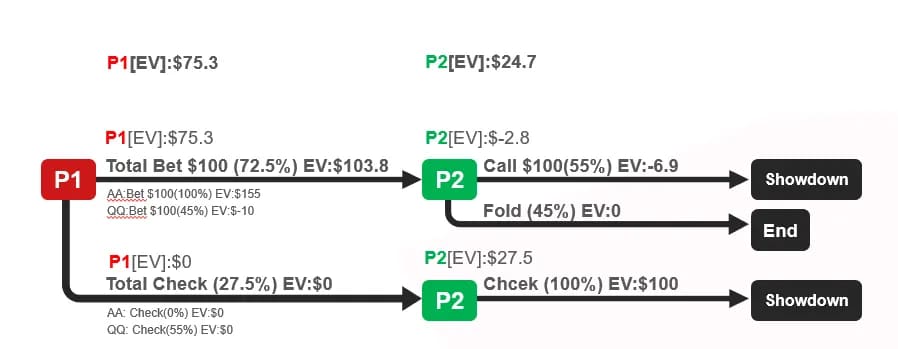
我们来看一下调整后的 EV 分配：P1 check 的频率从 25%上升到 27.5%，P2 在这条分支上同样收获底池全部 100bb；P1 bet 的频率从 75%下降到 72.5%，其中 A 占 50%，Q 占 22.5%，下注后 P2 跟注频率从 50%上升到 55%，进而导致 P2 在 P1 bet 后 fold EV 依旧等于 0。

但是 call 的 EV 从 0 变为-6.9，从而使得 P1 虽然更少的进入 bet 这个分支，但在个分支上每次收益从 100bb 上升到 103.8bb。P1 的总体 EV 从 75 上升到 75.3，P2 的总体 EV 从 25，下降到 24.7。

如何打疯狂咋呼老板

有了刚刚的分析，我们可以快构建另一种场景的数学模型：P2 是理智玩家，但是 P1 偏爱诈唬。

P1 的认知偏差为：自己手持 Q 下注时（无论是否诈唬成功）都会获得额外 b 的情绪价值，而 P2 一旦弃牌就会损失 b。

EV 公式如下

EV(P2 Call)=300*x/(1+x)-100

EV(P2 Fold)=-b

EV(P1 Bet with Q)=(200)*(1-y)-100+b

EV(P1 Check with Q)=0

解得

y=(100-b)/200

x=(100-b)/(200+b)

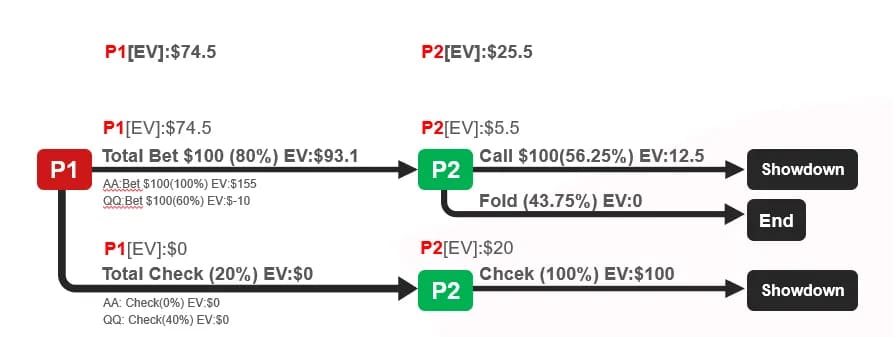
当 P2 观测到 P1 下注频率从 75%上升到 80%时，意味着 P1 手持 Q 是下注频率从 50%上升到 60%，进而可以解得 b=-12.25，y=56.25%。新的 EV 分布如下

知识点总结

博弈论基础

四要素：参与者、策略、信息、结果（+收益）

四种游戏类型：完美信息静态博弈（囚徒困境）、非完美信息静态博弈（医药）、完美信息动态博弈（围棋）、非完美信息动态博弈（德州扑克）

纳什均衡：任何一个参与者单独偏离均衡点，均不会导致自己的结果变好

AKQ Toy Game

双方范围 equity 相同时，EV 不一定相同